Условие задачи
В call-центре имеется 10 операторов, время обслуживания заявки имеет экспоненциальное распределение со средним значением 45 с. Ответить на следующие вопросы, относящиеся к обслуживанию заявок.
1. Заявка, получившая отказ, теряется. Найти среднее время до освобождения всех операторов, если новые заявки не поступают.
2. Заявка, получившая отказ, становится на ожидание. Найти среднее время до освобождения всех операторов, если в данный момент число обслуживаемых и ожидающих пользователей равно 15 и новые заявки не поступают.
3. Заявка, получившая отказ, становится на ожидание. На обслуживании и ожидании находятся 11 заявок. Найти вероятность того, что ожидающая заявка будет обслужена последней (первой).
Ответ
1. Поскольку новые заявки не поступают, плотность вероятности продолжительности времени до реализации первого события (в нашем случае до освобождения одного из десяти занятых операторов) определяется из выражения:
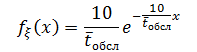
Тогда математическое ожидание этой величины (среднее время до освобождения первого оператора) есть:
