Главная
Библиотека
Теория вероятностей
В результате опыта получена выборочная совокупность. 1. По данной таблице составить интервальный вариационный ряд, разбив...

В результате опыта получена выборочная совокупность. 1. По данной таблице составить интервальный вариационный ряд, разбив всю вариацию на 8-10 интервалов. 2. По сгруппированным данным построить: полигон относительных частот; гистограмму относительных

«В результате опыта получена выборочная совокупность. 1. По данной таблице составить интервальный вариационный ряд, разбив всю вариацию на 8-10 интервалов. 2. По сгруппированным данным построить: полигон относительных частот; гистограмму относительных»

24 декабря 2023
Теория вероятностей

Условие:

В результате опыта получена выборочная совокупность.

1. По данной таблице составить интервальный вариационный ряд, разбив всю вариацию на 8-10 интервалов.

2. По сгруппированным данным построить:

полигон относительных частот;
гистограмму относительных частот;
график эмпирической функции распределения.

3. Найти числовые характеристики выборочной совокупности: выборочную среднюю 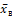, выборочную дисперсию 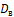, выборочное среднее квадратическое отклонение 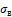и исправленную дисперсию .

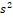4. По виду гистограммы и эмпирической функции распределения выборки выдвинуть гипотезу о распределении генеральной совокупности.

5. Проверить выполнение правила «трёх сигм».

6. Применив критерий согласия Пирсона 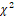с заданным уровнем значимости 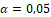, окончательно принять или отвергнуть выдвинутую гипотезу о распределении генеральной совокупности.

7. Найти доверительные интервалы для генеральной средней и генерального среднего квадратического отклонения по уровню надёжности .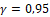

Решение:

1.По данной таблице составить интервальный вариационный ряд, разбив всю вариацию на 8-10 интервалов.
Разобьем всю вариацию объемом 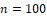на частичных интервалов равной длины и посчитаем частоты попадания наблюдаемых значений в частичные интервалы.