В сборочном цехе завода было произведено выборочное обследование зарплаты рабочих и получены следующие результаты (в тыс. р.): Требуется: 1) найти выборочную среднюю; 2) составить интервальное распределение выборки с шагом h
- Теория вероятностей
Условие:
В сборочном цехе завода было произведено выборочное обследование зарплаты рабочих и получены следующие результаты (в тыс. р.):

Требуется:
1) найти выборочную среднюю;
2) составить интервальное распределение выборки с шагом h, взяв за начало первого интервала х0;
3) построить полигон и гистограмму частот;
4) проверить с помощью критерия Пирсона при заданном уровне значимости α гипотезу о том, что случайная величина μ – количественный признак генеральной совокупности - имеет нормальное распределение;
5) найти с надёжностью γ доверительный интервал для оценки неизвестного математического ожидания признака μ генеральной совокупности.
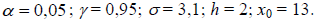
Решение:
Объем выборки n = 25.
Выборочная средняя вычисляется по формуле:
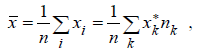
где xi элемент выборки;
nj эмпирические частоты;
x* j середина j-го интервала.
Сначала составим интервальное распределение выборки с шагом h = 2, взяв за начало первого интервала x0 = 13 .
Границы интервалов разбиения определяются по формулам:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства