Условие:
Вероятность того, что непрерывная случайная величина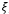 
, распределенная по показательному закону, принимает значения больше 60, равна 
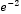. Найти плотность распределения случайной величины 
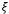, функцию распределения, построить графики этих функций. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины 
.
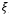Решение:
Функция показательного распределения имеет вид
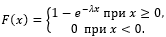
Из условия
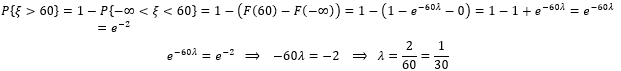
Функция распределения имеет вид