Время пребывания заявки на ожидании ограничено случайной величиной, имеющей экспоненциальное распределение с параметром ку. Определить необходимые характеристики и используя формулу Литтла.
«Время пребывания заявки на ожидании ограничено случайной величиной, имеющей экспоненциальное распределение с параметром ку. Определить необходимые характеристики и используя формулу Литтла.»
- Теория вероятностей
Условие:
Время пребывания заявки на ожидании ограничено случайной величиной, имеющей экспоненциальное распределение с параметром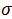 
. Определить необходимые характеристики и используя формулу Литтла, получить выражение для среднего времени пребывания заявки на ожидании начала обслуживания. Получить аналогичное выражение по результатам анализа длины очереди только для заявок, попавших на ожидание.
Решение:
Начинаем с построения графа состояний этой СМО (обозначения аналогичны предыдущему номеру):
Последовательно выражаем вероятности состояний СМО через вероятность отсутствия заявок в СМО.
Первые состояний не отличаются от предыдущей задачи, потому сразу записываем:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э