1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. Выборка икс объемом н равно 100 измерений. По критерию...
Решение задачи на тему

Выборка икс объемом н равно 100 измерений. По критерию икс в квадрате проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости альфа равно ноль целых пять сотых. m_(x_4 )=30-(2+1)=27

  • Теория вероятностей
Выборка икс объемом н равно 100 измерений. По критерию икс в квадрате проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости альфа равно ноль целых пять сотых. m_(x_4 )=30-(2+1)=27

Условие:

Выборка X объемом N=100 измерений задана таблицей 1.

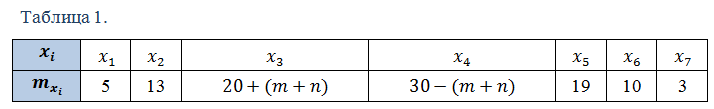
где xi – результаты измерений, mxi  – частоты, с которыми встречаются значения xi, ∑i=17mxi =100. Значения xi рассчитываются по формуле xi=0,2∙m+(i-1)∙0,3∙n.

1. Построить полигон относительных частот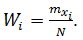

2.   Вычислить выборочное среднее 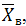  выборочную дисперсию 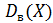и среднее квадратическое отклонение .

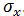3.   По критерию 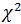проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости α=0,05. 

Решение:

Последние цифры шифра 56, соответственно m=2, n=1.

Тогда:

x1=0,2∙2+(1-1)∙0,3∙1=0,4

x2=0,2∙2+(2-1)∙0,3∙1=0,4+0,3=0,7

x3=0,2∙2+(3-1)∙0,3∙1=0,4+0,6=1

x4=0,2∙2+(4-1)∙0,3∙1=0,4+0,9=1,3

x5=0,2∙2+(5-1)∙0,3∙1=0,4+1,2=1,6

x6=0,2∙2+(6-1)∙0,3∙1=0,4+1,5=1,9

x7=0,2∙2+(7-1)∙0,3∙1=0,4+1,8=2,2

mx3=20+(2+1)=23

mx4=30-(2+1)=27

Таким образом, получили следующую выборку результатов измерений (Таблица 2):

Полигон отно...

Похожие задачи

Не нашел нужную задачу?Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я