Х – месячный доход жителя региона (в руб.) Считая, что таблица 3а) представляет распределение по месячному доходу 1000 жителей, отобранных по схеме собственно-случайной бесповторной выборки для исследования доходов населения города, составляющего 20 000
- Теория вероятностей
Условие:
Х – месячный доход жителя региона (в руб.)

Считая, что таблица 3а) представляет распределение по месячному доходу 1000 жителей, отобранных по схеме собственно-случайной бесповторной выборки для исследования доходов населения города, составляющего 20 000 человек, решить следующие задачи:
1) Найти вероятность того, что средний месячный доход жителя города отличается от среднего дохода в выборке не более, чем на 45 (по абсолютной величине).
2) Определить границы, в которых с надежностью 0,99 заключен средний месячный доход жителя города.
3) Каким должен быть объем выборки, чтобы те же границы гарантировать с надежностью 0,9973?
4) Решить задачи 1) – 3), если население города неизвестно, но очень велико по сравнению с объемом выборки.
5) Найти вероятность того, что доля малообеспеченных жителей города (доход менее 500) отличается от доли таких же жителей в выборке не более, чем на 0,01 (по абсолютной величине).
6) Определить границы, в которых с надежностью 0,98 заключена доля малообеспеченных жителей города
7) Каким должен быть объем выборки, чтобы те же границы для доли малообеспеченных жителей города гарантировать с надежностью 0,9973?
8) Как изменились бы результаты, если бы о доле малообеспеченных жителей вообще ничего не было бы известно?
9) Решить задачи 5) – 8), если население города неизвестно, но очень велико по сравнению с объемом выборки.
Решение:
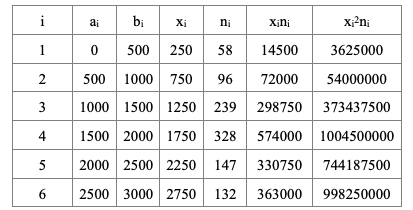

Рассчитаем средние значения указанных интервалов: соответственно, начало и конец i-го интервала, (первый и последний интервал будем
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства