Условие задачи
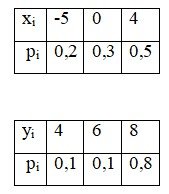
Заданы две независимые дискретные случайные величины X и Y своими рядами распределения. Найдите:
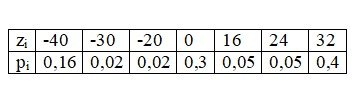
1) ряд распределения для случайной величины Z = X*Y;
2) функцию распределения случайных величин X; Y; Z;
3) числовые характеристики: математическое ожидание, дисперсию и среднее квадратическое отклонение случайных величин X; Y; Z и проверьте выполнимость свойств для математического ожидания и дисперсии (где это возможно);
4) постройте многоугольники распределения и графики функции распределения для случайных величин X; Y; Z.
Ответ
Z = XY
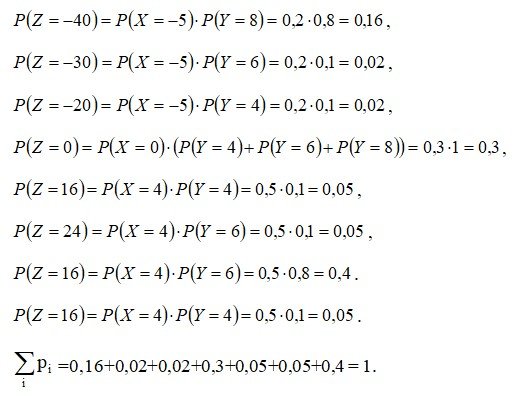
2. Функция распределения СВ Х:
F(х) = P(Xx).
При х -5, F(х) = 0.
При -5 х 0, F(х) = 0,2.
При 0 х 4, F(х) = 0,2+ 0,3= 0,5.
При х 4, F(х) = 0+ 0,2 + 0,3 + 0,5= 1.
Потяни
