Затраты x1 первого основного цеха завода от цикла к циклу описываются разностным уравнением первого порядка вида: а затраты x2 второго (вспомогательного) цеха описываются разностным уравнением вида:
- Управление проектами
Условие:
Затраты x1 первого основного цеха завода от цикла к циклу описываются разностным уравнением первого порядка вида:
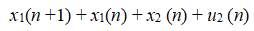
а затраты x2 второго (вспомогательного) цеха описываются разностным уравнением вида:
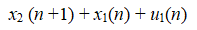
Заданы начальное и конечное состояния системы и интервал управления системой
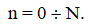
Проблема
Перед руководством завода стоит проблема: так изменять управление цехами u1 и u2 (изменять затраты), чтобы на интервале управления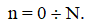 
выполнялось условие минимума интегральной целевой функции
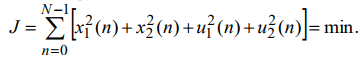
Эта функция учитывает затраты цехов x1 и x2 на каждом цикле, а также изменение затрат, вызванных величинами u1 и u2. Известно, что изменение объема производства в ту или иную сторону влечет увеличение потерь, связанных с перестройкой производства. Терминальная функция F в этой задаче равна нулю.
Вам предлагается описать возможные варианты решений, выбрать наиболее оптимальное и обосновать, почему Вы считаете это решение оптимальным.
Решение:
Данный кейс решается, как система уравнений третьего порядка и показывает распределение на работу затрат такси по телефону.
Произведем решение системы уравнений.
Решим первое уравнение:
Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$x_{1} = \frac{\sqrt{D} - b}{2 a}$
$x_{2} = \frac{- \sqrt{D} - b}{2 a}$
где D = b^2 - 4*a*c - это дискриминант.
Т.к.
$a = 1$
$b = 2$
$c = 1$
, то
D = b^2 - 4 * a * c = (2)^2 - 4 * (1) * (1) = 0
Т.к. D = 0, то корень всего один.
x = -b/2a = -2/2/(1)
$x_{1} = -1$
Решим второе уравнение системы:
Эт...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства