1. Если две дифференцируемые функции отличаются на постоянное слагаемое, то Их производные равны Их производные различаются на разность постоянных слагаемых Вопрос о различии их производных установить не удаётся

1. Если две дифференцируемые функции отличаются на постоянное слагаемое, то

Их производные равны
Их производные различаются на разность постоянных слагаемых
Вопрос о различии их производных установить не удаётся
Следует применять правило дифференцирования сложной функции
 

2. Дифференцируемая функция может иметь экстремум в тех точках, где

Производная не существует
Производная равна нулю
Производная равна нулю или не существует
Производная меньше нуля
 

3. Что из ниже приведённого не является видом асимптот:

Вертикальные
 Горизонтальные
 Касательные
Наклонные
 

4. Область определения функции двух переменных может быть представлена:

отрезками на осях Ox и Oy
множеством точек плоскости xOy
отрезком на оси Oz
точкой x на оси Ox и точкой y на оси Oy
 

5. Область определения функции 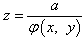  - это

все точки плоскости, в которых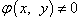  
вся плоскость xOy
 вся плоскость yOz
все точки плоскости, в которых φ(x,y)>0
 

6. Производная по направлению является:

линейной комбинацией частных производных
обычной частной производной
тем же, что градиент функции
производной по одному аргументу
 

7. Точки экстремума функции двух переменных - это:

точки, в которых первые частные производные равны нулю или не существуют
точки, которые находятся в верхней полуплоскости
точки, которые не могут быть изображены графически
очки пересечения с осями координат
 

8. Чтобы найти стационарную точку функции z = f(x, у), надо решить систему

9. Полное приращение функции z = f(x, у) имеет вид
  

 

10. Частное приращение функции z = f(x, у) по переменной у имеет вид
  

 

11. Угловой коэффициент касательной, проведенной к графику функции в некоторой точке, равен

отношению значения функции к значению аргумента в этой точке;
значению производной функции в этой точке;
значению дифференциала функции в этой точке;
значению тангенса производной функции в этой точке
 

12. На рис. изображен график функции f(x). Тогда производная f'(x) это

 

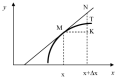
13. Дифференциал функции равен

 отношению приращения функции к приращению аргумента;
произведению приращения функции на приращение аргумента;
произведению производной на приращение аргумента;
приращению функции;
 

14. Дифференциал постоянной равен...

этой постоянной;
бесконечно большой величине
нулю;
невозможно определить.
 

15. Для любой линейной функции верно, что дифференциал этой функции равен

приращению функции;
постоянной величине
приращению аргумента;
производной функции.
 

16.Для дифференцируемой функции f(x) достаточное условие выпуклости (выпуклости вверх) имеет вид

17. Для дифференцируемой функции f(x) достаточное условие выпуклости (выпуклости вниз) имеет вид

 

18. Для дифференцируемой функции f(x) необходимое условие точки перегиба имеет вид

19. График функции у = f(x), удовлетворяющей условиям 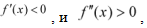  изображен на рисунке:
  

20. Для функции 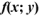   всякая точка  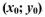  в которой выполняется условие  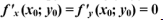, является 

точкой экстремума
точкой разрыв
стационарной точкой;
граничной точкой
 

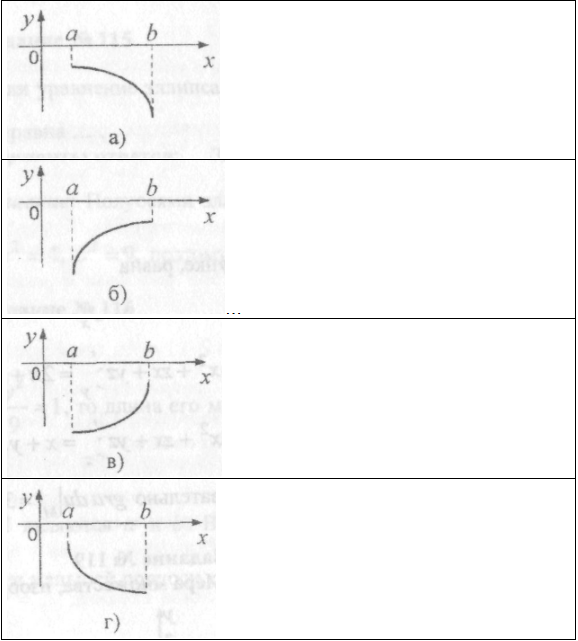
21. Укажите вид графика для которого на отрезке 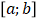  одновременно выполняются условия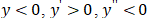    

 

 22. Дан график производной некоторой функции 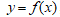 , заданной на отрезке  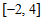. Тогда справедливы следующие утверждения:

 
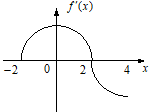
функция возрастает на заданном промежутке;
функция убывает на заданном промежутке;
функция возрастает на промежутке (–2, 2) и убывает на промежутке (2, 4);
На всем промежутке функция выпукла вверх
 

 23. Дан график производной некоторой функции 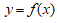 , заданной на промежутке [0, 4]. 

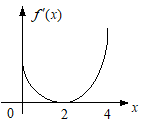
Тогда не верными являются следующие утверждения:

на всем промежутке график функции имеет направление выпуклости вниз;
на всем промежутке функция не убывает;
график функции имеет перегиб в точке  .
На всем промежутке функция убывает.