Решение задачи
Численно решить задачу Коши для обыкновенного дифференциального уравнения 1-го порядка на отрезке с шагом h=0.2: y^'=f(t,y)=(3t+1)/(t+1) y+3t,y(1)=0 а) методом Эйлера;
- Высшая математика
Условие:
Численно решить задачу Коши для обыкновенного дифференциального уравнения 1-го порядка на отрезке с шагом h=0.2:

а) методом Эйлера;
б) методом Рунге-Кутты 2-го порядка точности с оценкой погрешности по правилу Рунге. Найти точное решение задачи. Построить на одном чертеже графики точного и приближённых решений.
Решение:
а) Приближенное решение в узлах ti, которое обозначим через yi, определяется по формуле
yi+1 = yi + hf(ti, yi ),
ti = 1+ih, i=0,1,,5
Сведём вычисления в таблицу:
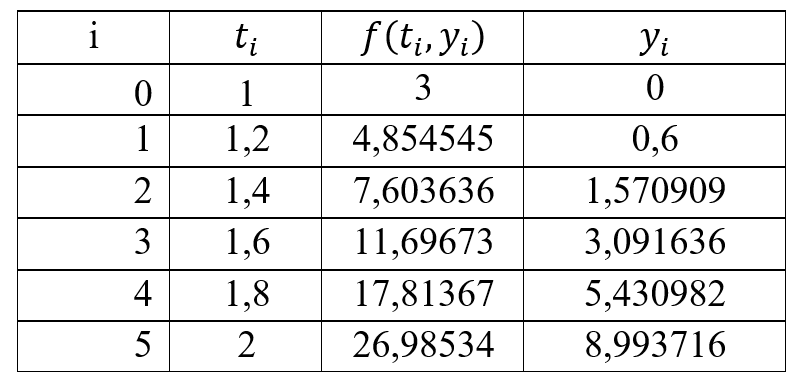
б) Метод Рунге-Кутта второго порядка точности (h=0.2)
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э