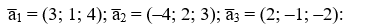Условие:
Даны векторы a̅1, a̅2, a̅3, b¯.
Показать, что векторы a̅1, a̅2, a̅3 образуют базис трехмерного пространства и найти координаты вектора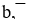 
в этом базисе.
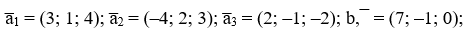
Решение:
Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля. В противном случае вектора не являются базисными и никакой вектор нельзя разложить по данному базису.
Вычислим определитель, столбцами которого являются координаты данных векторов
