Для таблично заданной функции найти аппроксимирующий (второй степени) и интерполяционный многочлены, а также построить их графики и соответствующие ломаные линии. Вычислить с помощью найденных многочленов приближенные значения функции
«Для таблично заданной функции найти аппроксимирующий (второй степени) и интерполяционный многочлены, а также построить их графики и соответствующие ломаные линии. Вычислить с помощью найденных многочленов приближенные значения функции»
- Высшая математика
Условие:
Для таблично заданной функции найти аппроксимирующий (второй степени) и интерполяционный многочлены, а также построить их графики и соответствующие ломаные линии. Вычислить с помощью найденных многочленов приближенные значения функции при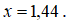 
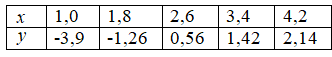
Решение:
При аппроксимации таблично заданных значений воспользуемся методом наименьших квадратов.
Для данных таблицы методом наименьших квадратов подобрать квадратичную функцию.
Для квадратичной функции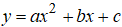 
необходимо найти параметры , решив систему уравнений. Вычислим коэффициенты системы:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э