Функция разложена в ряд Лорана в окрестности своей изолированной особой точки. Определите тип особой точки и найдите в ней вычет функции.
«Функция разложена в ряд Лорана в окрестности своей изолированной особой точки. Определите тип особой точки и найдите в ней вычет функции.»
- Высшая математика
Условие:
Функция f(z) разложена в ряд Лорана в окрестности своей изолированной особой точки z0, где 0<|z-z_0 |<R.
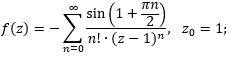
А) Определите тип особой точки z0 и найдите в ней вычет функции f(z).
Б) Вычислите с помощью вычетов интеграл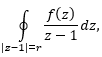
, если 0<r<R.
Решение:
Известно, что если ряд Лорана для функции f(z) в окрестности изолированной особой точки z0 не содержит главной части, то точка z0 является устранимой особой точкой; если главная часть ряда Лорана содержит конечное число слагаемых, то z0 - полюс; если же главная часть ряда Лорана содержит бесконечное число слагаемых, то z0 - существенно особая точка.
Для заданного ряда имеем:
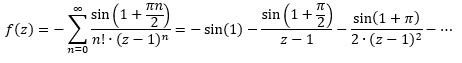
Очевидно, что в глав...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э