Используя аддитивность определенного интеграла, вычислите Теперь определим значение в промежутках между этими точками. Построим график функции
«Используя аддитивность определенного интеграла, вычислите Теперь определим значение в промежутках между этими точками. Построим график функции»
- Высшая математика
Условие:
Используя аддитивность определенного интеграла, вычислите
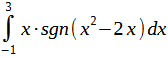
Решение:
Аддитивность определенного интеграла позволяет интегрировать не только непрерывные функции, но и те функции, которые в пределах промежутка интегрирования терпят конечный разрыв.
Свойство аддитивности. Если функция f(x) интегрируема на интервалах [a,c] и [c,b],
a c b, то она интегрируема и на интервале [a,b], при этом выполняется равенство
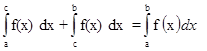
Вернемся к нашему примеру
Функция сигнум х определена следующим...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э