Условие:
Исследовать систему линейных алгебраических уравнений и, если она совместна, то найти её общее решение и одно частное решение.
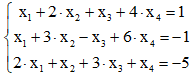
Решение:
При исследовании системы линейных алгебраических уравнений на совместность применяется теорема Кронекера-Капелли: если ранг матрицы системы равен рангу расширенной матрицы системы, то система совместна, причём, если ранг совпадает с количеством неизвестных, то решение единственно, а если ранг меньше количества неизвестных, то система имеет бесчисленное множество решений.
Для нашей задачи ранги матрицы системы и расширенной матрицы системы найдем методом Гаусса. При этом с помощью элементарных преобразований матрица приводится к ступенчатому виду, в результате чего выявляются и удаляются линейно...