Условие:
Капитану теплохода необходимо найти кратчайший путь из порта А в порт В. На отрезке АВ находится центр круглого острова (рис. 2.1). Каков должен быть маршрут теплохода? Докажите, что найденный путь действительно кратчайший.
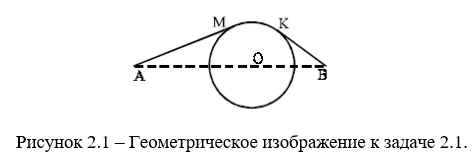
Решение:
Ответ угадывается достаточно просто: надо из точек А и В провести касательные к окружности AM и ВК так, чтобы точки М и К лежали по одну сторону прямой АВ. Кратчайший маршрут из А в В будет состоять из отрезка AM, дуги МК и отрезка КВ. Другой маршрут такой же длины получится, если отразить линию АМКВ симметрично относительно прямой АВ. Ясно, что достаточно рассмотреть только полуплоскость по одну сторону от прямой АВ.
Теперь надо доказать, что длина любого иного маршрута в рассматриваемой полуплоскости будет больше. Перебирать все возможные варианты и доказывать это для каждого конкретного пути...
