Классифицировать задачи оптимального управления. Вывести краевую задачу принципа максимума для модели из одного уравнения.Вывести краевую задачу принципа максимума для модели из системы ДУ.
«Классифицировать задачи оптимального управления. Вывести краевую задачу принципа максимума для модели из одного уравнения.Вывести краевую задачу принципа максимума для модели из системы ДУ.»
- Высшая математика
Условие:
Классифицировать задачи оптимального управления.
Вывести краевую задачу принципа максимума для модели из одного уравнения.
Вывести краевую задачу принципа максимума для модели из системы ДУ.
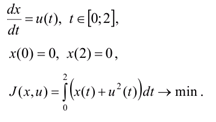
Решение:
По виду краевых условий эта задача с фиксированными концами.
По времени начала и окончания процесса эта задача с фиксированным временем, так как начальный t0 и конечный tf моменты фиксированы.
По критерию оптимальности это задача Лагранжа: при этом критерий имеет вид

Составим функцию Гамильтона Понтрягина.
H = - f0 + f = - (x + u2) + u ,
где должна быть решением сопряженного уравнения
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э