Главная
Библиотека
Высшая математика
Найти нижнюю и верхнюю оценки прибыли компании. С помощью сведения игры к задаче линейного программирования определить опт...

Найти нижнюю и верхнюю оценки прибыли компании. С помощью сведения игры к задаче линейного программирования определить оптимальную смешанную стратегию компании. Какой маршрут окажется наиболее предпочтительным?

«Найти нижнюю и верхнюю оценки прибыли компании. С помощью сведения игры к задаче линейного программирования определить оптимальную смешанную стратегию компании. Какой маршрут окажется наиболее предпочтительным?»

6 ноября 2024
Высшая математика

Условие:

Директор транспортной компании А, оказывающей транспортные услуги по перевозке пассажиров в областном центре, планирует открыть один или несколько маршрутов: А₁, А₂, … . Для этого было закуплено 100 микроавтобусов. Он может поставить весь транспорт на одном из маршрутов (наиболее выгодном), либо распределить по нескольким маршрутам. Спрос на транспорт, а соответственно и прибыль компании во многом зависит. от того, какие маршруты в ближайшее время откроет главный конкурент –компания В. Ее руководство полностью владеет ситуацией и может открыть несколько маршрутов В₁, В₂, … . Оценки прибыли компании А (млн. руб.) при любом ответе В представлены платежной матрицей:

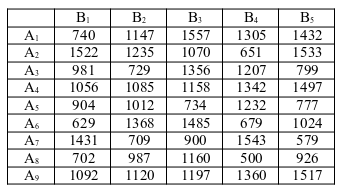
Требуется:

Найти нижнюю и верхнюю оценки прибыли компании.
С помощью сведения игры к задаче линейного программирования определить оптимальную смешанную стратегию компании. Какой маршрут окажется наиболее предпочтительным?
Вычислить оптимальную прибыль (убыток) компании при использовании оптимальной смешанной стратегии.

Решение:

1. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.Иногда на основании простого рассмотрения матрицы игры можно сказать, что некоторые чистые стратегии могут войти в оптимальную смешанную стратегию лишь с нулевой вероятностью.Говорят, что i-я стратегия 1-го игрока доминирует его k-ю стратегию, если aij akj для всех j Э N и хотя бы для одного j aij akj. В этом случае говорят также, что i-я стратегия (или строка) доминирующая, k-я доминируемая.Говорят, что j-я стратегия 2-го игрока доминирует его l-ю стратегию, если для всех j Э M aij ail и хотя бы для одного i aij...