Условие:
Найти общее решение дифференциального уравнения:
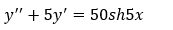
Решение:
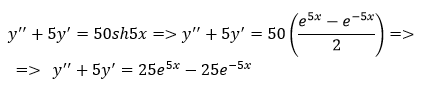
Сначала найдем общее решение соответствующего однородного уравнения
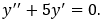
Для этого определим корни характеристического уравнения:

Найти общее решение дифференциального уравнения:
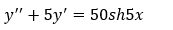
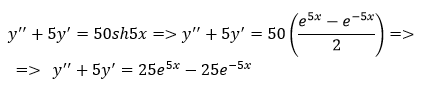
Сначала найдем общее решение соответствующего однородного уравнения
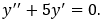
Для этого определим корни характеристического уравнения:
Не нашел нужную задачу?