👋 Решение задач
📚 Высшая математика
решение задачи на тему:
Дата добавления: 07.10.2024
Найти оптимальное неотрицательное решение максимизирующее линейную форму L=2x1-x4 при системе ограничений:
Ответ
Матрица системы:
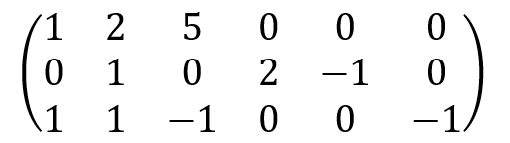
Ранг матрицы равен 3 и он совпадает с рангом расширенной матрицы. Значит система совместна, и три переменные можно выразить через другие три.
Выразим переменные x1 ,x3, x4:
Сводка по ответу
Купи подписку Кампус+ и изучай ответы
Материалы со всех ВУЗов страны
1 000 000+ полезных материалов
Это примеры на которых можно разобраться
Учись на отлично с библиотекой
Набор самых полезных инструментов, работающих на искусственном интеллекте для студентов всего мира.
Экосистема
Кампус
Экосистема сервисов для учебы в удовольствие
Hit
Кампус AI
Твой второй пилот в учебе, быстрые ответы на основе AI
Hit
Кампус Эксперт
ТОП-эксперты помогут решить и объяснят тебе любой вопрос по учебе онлайн
NEW
Кампус Чатс
Сообщество, где ты найдешь знакомства и получишь помощь
Hit
Кампус Хаб
Мультифункциональный умный бот, который всегда под рукой
NEW
Библиотека
База знаний из 1 000 000+ материалов для учебы
