Условие задачи
Найти решение задачи, используя геометрическую интерпретацию.
Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в следующей таблице:
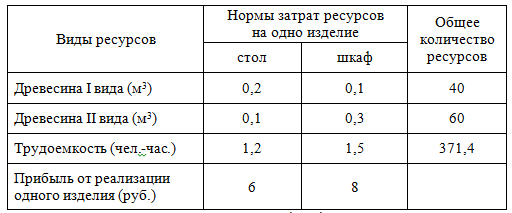
Определить, сколько столов и шкафов фабрике следует изготовлять, чтобы прибыль от их реализации была максимальной.
Решение.
1). Составляем математическую модель нашей задачи.
Вводим обозначения для количеств изготавливаемой мебели:
x1 – количество изготавливаемых столов (штук);
x2 – количество изготавливаемых шкафов (штук).
При этом прибыль от их реализации составит
F = 6·x1 + 8·x2 руб.
Целью решения задачи является определение среди всех допустимых таких значений x1 и x2, которые обеспечивают максимальную прибыль.
Ответ
Количества изготавливаемой мебели не могут быть отрицательными, поэтому x1 0, x2 0. Кроме того, по смыслу задачи, x1 и x2 целочисленные.
Другие ограничения задачи связаны с имеющимися ресурсами.
Математическая запись указанных ограничений такова:
0,2x1 + 0,1x2 40 имеющийся ресурс древесины вида I не может быть превышен, м3;
0,1x1 + 0,3x2 60 имеющийся ресурс древесины вида II не может быть превышен, м3;
1,2x1 + 1,5x2 371,4 имеющийся ресурс трудоёмкости не может быть превышен, чел.-час.
В целом соотношения математической модели задачи об оптимальных количествах изготавливаемой мебели выглядят...
