Найти случайную величину n - стоимость восстановления прибора за период времени Т: построить ряд и функцию распределения, вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение.

22 января 2025
Высшая математика

Условие:

Прибор состоит из двух независимо работающих блоков А и В, каждый из которых собран из нескольких независимых элементов (рис.1), вероятности отказов которых

р₁ = р₂= 0.2, р₃ = р₄ = р₇ = 0.3; р₅ = р₆ = 0.25, р₈= 0.278

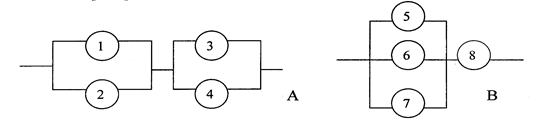
Рис 1

При отказе блока он подлежит полной замене, причем стоимость замены блока А равна С₁ = 5 единицам стоимости, блока В – С₂= 10 единиц. Предполагается, что за определенный период времени Т ни один блок не потребует повторной замены.

Найти случайную величину n - стоимость восстановления прибора за период времени Т:

1) построить ряд и функцию распределения,

2) вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение,

3) построить многоугольник распределения и график функции распределения.

Решение:

Определим значения случайной величины n, которая является дискретной. Случайная величина n стоимость ремонта может принимать только четыре значения.

х₁ = 0 - ни один блок не потребует замены;

х₂= С₁ = 5 - только блок А потребует замену;

х₃ = С₂ = 10 - только блок В потребует замену;

х₄ = С₁ +С₂ = 15 - оба блока потребуют замену.

Чтобы вычислить вероятность каждого из значений х_i, следует сначала найти вероятности выхода из строя блоков А и В.

Обозначим А - выход из строя блока А, Ai отказ i-го элемента (i = 1,2,3,4). Блок А откажет, если откажет хотя бы одна из его частей (первая часть со...