Условие задачи
Непрерывная случайная величина задана интегральной функцией распределения F(x).
Требуется найти:
1) дифференциальную функцию распределения f(x) (плотность вероятности);
2) математическое ожидание М(Х);
3) дисперсию D(Х) и среднее квадратическое отклонение σ(Х);
4) вероятность попадания заданной случайной величины Х в заданный интервал P(α<X<β);
5) построить график интегральной функции распределения;
6) построить график дифференциальной функции распределения.
Ответ
1) по определению функции плотности вероятности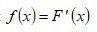 
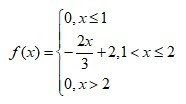
График дифференциальной функции f(x) (плотность вероятности)
Потяни
