Условие задачи
Ниже приведены числовые данные задачи линейного программирования, записанные в виде таблицы
которые эквивалентны следующей записи:
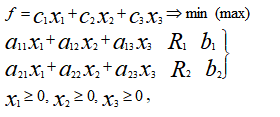
где R1, R2 — один из знаков «≤» или «≥».
Необходимо выполнить последовательно следующие задания:
1. Применяя симплекс-метод, решить задачу или установить, что задача не имеет решения. В последнем случае указать причину неразрешимости: а) множество решений пусто; б) целевая функция не ограничена на заданном множестве решений. Если существуют альтернативные оптимальные планы, следует найти общее оптимальное решение.
2. Построить двойственную задачу. Если прямая задача разрешима, то найти оптимальное решение двойственной задачи, применяя первую теорему двойственности. Сравнить значения функций, соответствующих оптимальным планам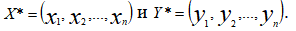 
3. Решить графическим методом двойственную задачу и, применяя условия дополняющей нежесткости, найти оптимальное решение прямой задачи. Сравнить результат с результатом, полученным симплекс-методом.
Ответ
1. Применяя симплекс-метод, решим задачу или установим, что задача не имеет решения.
Определим минимальное значение целевой функции
F(X) = 2x1-22x2+72x3
при следующих условиях-ограничениях:
x1-3x2+x35;
x1+5x2-9x32.
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
1x1-3x2 + 1x3-1x4 + 0x5 = 5
1x1 + 5x2-9x3 + 0x4 + 1x5 = 2
Введем искусственные переменные x: в 1-м равенстве вводим переменную x6:
1x1-3x2 + 1x3-1x4 + 0x5 + 1x6 = 5
1x1 + 5x2-9x3 + 0x4 + 1x5 + 0x6 = 2
Для по...
