1. Главная
  2. Библиотека
  3. Высшая математика
  4. Определим последовательность функций Fn: N→ N, n ∈ N: F0(x) = x + 1; Fn+1(x) = Fn(Fn(…Fn(1)…)), где справа функция Fn прим...

Определим последовательность функций Fn: N→ N, n ∈ N: F0(x) = x + 1; Fn+1(x) = Fn(Fn(…Fn(1)…)), где справа функция Fn применяется x + 1 раз. Докажите: F1(x + 1 ) = F0(F1(x)); Fn+1(x + 1 ) = Fn(Fn+1(x)); F1(x) = x + 2; F3(x) = 2x + 3 – 3.

«Определим последовательность функций Fn: N→ N, n ∈ N: F0(x) = x + 1; Fn+1(x) = Fn(Fn(…Fn(1)…)), где справа функция Fn применяется x + 1 раз. Докажите: F1(x + 1 ) = F0(F1(x)); Fn+1(x + 1 ) = Fn(Fn+1(x)); F1(x) = x + 2; F3(x) = 2x + 3 – 3.»
  • Высшая математика

Условие:

   Функция Аккермана.
Определим последовательность одноместных функций Fn: N→ N, n ∈ N следующим образом:

F0(x) = x + 1; 
Fn+1(x) = Fn(Fn(…Fn(1)…)), 

где справа функция Fn применяется x + 1 раз.
   

   Докажите:

1) F1(x + 1 ) = F0(F1(x));
2) Fn+1(x + 1 ) = Fn(Fn+1(x));
3) F1(x) = x + 2;
4) F2(x) = 2x + 3; 
5) F3(x) = 2x + 3 – 3;

6) F4(x) =

Решение:

1. Имеем в силу равенства Fn+1(x) = Fn(Fn(Fn(1))):

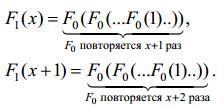
Поэтому получаем F1(x + 1 ) = F0(F1(x)).

2. Проводим математическую индукцию по n. Базис индукции для n = 0 доказан в пункте 1). Для доказательства индуктивного перехода предположим, что для n = k выполнено Fk+1(x + 1 ) = Fk(Fk+1(x)). Имеем в силу равенства Fn+1(x) = Fn(Fn(Fn(1))):

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я