По критерию Пирсона при уровне значимости 0.025 проверить гипотезу о распределении случайной величины икс по закону ф от икс равно 1 минус икс минус 1 2 при икс 0, 1, если задано нк попаданий выборочных значений случайной величины икс.
«По критерию Пирсона при уровне значимости 0.025 проверить гипотезу о распределении случайной величины икс по закону ф от икс равно 1 минус икс минус 1 2 при икс 0, 1, если задано нк попаданий выборочных значений случайной величины икс.»
- Высшая математика
Условие:
По критерию Пирсона при уровне значимости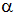 
= 0.025 проверить гипотезу о распределении случайной величины Х по закону F(x) =1–(x–1)2 при
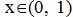, если задано nk попаданий выборочных значений случайной величины Х в подинтервал 
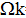= (ak , bk ):
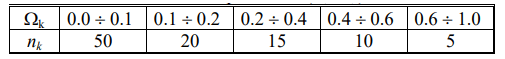
Решение:
Определим объем выборки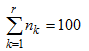 
Подсчитаем вероятности pk для предполагаемого нормального распределения случайной величины Х по формуле
, где ak и bkсоответственно нижняя и верхняя границы подинтервалов Добавим также строку плотностей частоты f*, деля nk на объем выборки n =100 и на длину подинтервала
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э