По предоставленным данным необходимо составить математическую модель задачи, решить задачу графическим и симплекс-методом.
- Высшая математика
Условие:
Составить математическую модель задачи, решить задачу графическим и симплекс-методом.
Для изготовления шкафов и буфетов мебельная фабрика использует древесину 4 видов D1 , D2 , D3 и D4 . Запасы древесины, нормы расхода древесины на производство единицы каждого вида изделия, а также прибыль от реализации единицы изделий приведены в таблице. Найти оптимальный план производства столов и шкафов, обеспечивающий максимальную прибыль.
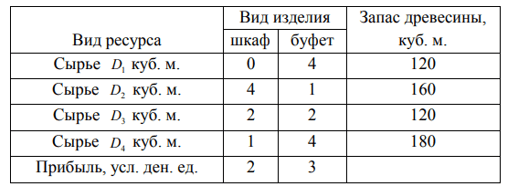
Решение:
Под планом производства будем понимать ответ на вопрос: сколько изделий А и сколько изделий В надо выпустить, чтобы прибыль была максимальна. Ведем переменные задачи: пусть x1 - объем выпуска шкафов, x2 - объем выпуска буфетов. Тогда на выпуск одного шкафа будет израсходовано 0х1+4х2куб.м. сырья Д1, 4х1+х2куб.м. сырья Д2, 2х1+2х2куб.м. сырья Д3 и 1х1+4х2куб.м. сырья Д4. Суммарная прибыль составит 2х1+3х2 денежных единиц. Так как нельзя израсходовать сырья больше, чем имеется, то математическая модель задачи будет иметь вид:
1) система ограничений:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства