Построить на плоскости область решения системы линейных неравенств и геометрически найти наименьшее и наибольшее значение функции f(x_1,x_2) {(x_1+〖3x〗_2≥2,@4x_1-2x_2≤35@〖5x〗_1-13x_2≥18)┤f(x_1,x_2 )=7x_1+x_2→extr
«Построить на плоскости область решения системы линейных неравенств и геометрически найти наименьшее и наибольшее значение функции f(x_1,x_2) {(x_1+〖3x〗_2≥2,@4x_1-2x_2≤35@〖5x〗_1-13x_2≥18)┤f(x_1,x_2 )=7x_1+x_2→extr»
- Высшая математика
Условие:
Построить на плоскости область решения системы линейных неравенств и геометрически найти наименьшее и наибольшее значение функции f(x1, x2)
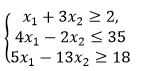
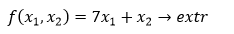
Решение:
Построим область допустимых решений, т.е. решим графически систему неравенств.
Границей неравенства x1+3x2 2 является прямая x1+3x2 = 2, построим ее по двум точкам:
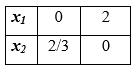
Произвольная точка (0; 0) не удовлетворяет неравенству x1+3x2 2, поэтому областью решения неравенства являются точки, лежащие выше прямой x1 +3x2 = 2. Область решения обозначим штриховкой.
Границей неравенства 4x1 - 2x2 35 явля...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э