Условие задачи
Предприятие выпускает два вида продукции A и B, для производства которых используется сырье трех видов. На изготовление единицы изделия A требуется затратить сырья каждого вида a1, a2, a3 кг соответственно, а для единицы изделия B - b1, b2, b3 кг. Производство обеспечено сырьем каждого вида в количестве P1, P2, P3 кг соответственно. Стоимость единицы изделия A составляет С1 руб., а единицы изделия B – С2 руб. Требуется составить план производства изделий A и B, обеспечивающий максимальную стоимость готовой продукции.
1) Решить задачу симплекс-методом.
2) Решить задачу геометрически.
a1 = 14, a2 = 14, a3 = 6;
b1 = 5, b2 = 8, b3 = 12;
P1 = 350, P2 = 392, P3 = 408;
С1 = 10, С2 = 5.
Ответ
Составим экономико-математическую модель задачи.
x1 количество продукции вида A, ед.
x2 количество продукции вида B, ед.
Математическая модель задачи имеет вид:
F(x)=10x1+5x2max
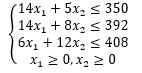
Решим задачу симплекс-методом
Приведем задачу к каноническому виду (для этого в каждое неравенство вводим дополнительную переменную со знаком плюс: x3,x4,x5).
F(x)=10x1+5x2max
