Рассмотреть задачу двухкритериальной оптимизации z_1=F_1 (x)=2x_1+5x_2+4x_3→max, z_2=F_2 (x)=-5x_1+x_2-4x_3→max, на множестве допустимых решений X∈E^3 2x_1^2+x_2^2+(x_3+1)^2≤1,
- Высшая математика
Условие:
Рассмотреть задачу двухкритериальной оптимизации
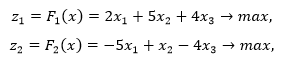
на множестве допустимых решений X ∈ E3
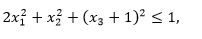
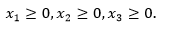
Найти Парето-эффективное решение, максимизирующее линейную свертку критериев
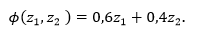
Проверить, выполняется ли для возникающей задачи нелинейного программирования условия теоремы Вейерштрасса и является ли эта задача задачей выпуклого программирования. Проверить возможность использования условий Куна-Таккера в данной задаче. Выписать и проверить выполнение условий Куна-Таккера в градиентной форме для различных наборов активных ограничений. Найти решение рассматриваемой задачи нелинейного программирования. Выписать функцию Лагранжа и условия Куна-Таккера через функцию Лагранжа; проверить выполнение условий Куна-Таккера в найденном решении.
Решение:
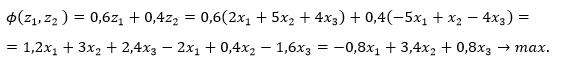
Ограничение
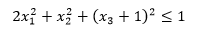
представляет собой эллипсоид с центром в точке ...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства