Три отрасли промышленности I, II и III являются производителями и в то же время потребителями некоторой продукции. Их взаимосвязь определяет матрица А коэффициентов прямых затрат

 Три отрасли промышленности I, II и III являются производителями и в то же время потребителями некоторой продукции. Их взаимосвязь определяет матрица А коэффициентов прямых затрат

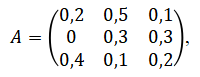
в которой число 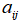 , стоящее на пересечении  i-ой строки и  j-го столбца равно  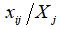, где 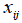  – поток средств производства из  i-ой отрасли в  j-ую, а  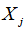 – валовой объем продукции  j-ой отрасли (все объемы продукции выражаются в единицах стоимости).

Задан также вектор 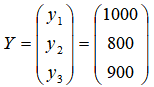  объемов конечной продукции.

1. Составить уравнение межотраслевого баланса.

2. Решить линейную алгебраическую систему уравнений межотраслевого баланса, то есть найти объемы валовой продукции каждой отрасли 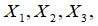  обеспечивающие потребности всех отраслей и изготовление конечной продукции Y. (Расчеты рекомендуется производить с точностью до четырех знаков после запятой)

3. Составить таблицу Х потоков средств производства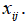  

4. Определить общие доходы каждой отрасли  .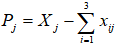

5. Результаты расчетов оформить в виде таблицы межотраслевого баланса:

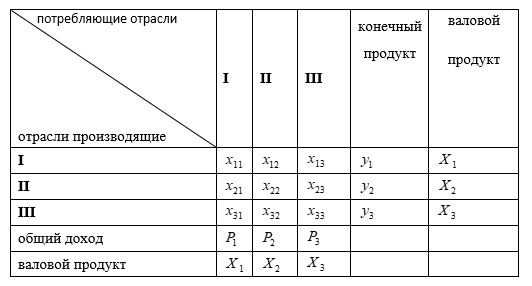
6. Найти матрицу коэффициентов полных затрат по формуле  , где Е – единичная матрица размера  .

7 ***. Рассчитать валовые выпуски 1-й и  2-ой отрасли  и конечный продукт 3-й отрасли  на планируемый период при условии увеличения конечного продукта 1-й и 2-й отрасли  на 8%, оставив без изменения объем валового продукта 3-й отрасли  .

Замечание. Показать явно

1) вычисление определителя матрицы Е-А;

2) вычисление обратной матрицы  ;

3) проверку путём вычисления произведения матрицы Е-А на обратную ей.