Условие задачи
В большой партии изделий 60% изделий высшего качества и 0,1% бракованных. Остальные изделия первого сорта. Найти вероятность того, что:
1) из 5 наугад отобранных изделий ровно два высшего качества;
2) из 5 наугад отобранных не более двух высшего качества;
3) из 5 наугад отобранных изделий хотя бы одно высшего качества;
4) среди 550 наугад отобранных изделий количество изделий высшего качества лежит в промежутке [280;310];
5) среди 550 наугад отобранных ровно 8 изделий высшего качества;
6) среди 550 наугад отобранных менее трех бракованных.
Ответ
1) Условие задачи можно рассматривать как серию из n=5 независимых испытаний, состоящих в проверке изделия, в каждом из которых с вероятностью p=0,6 может осуществиться событие, что изделию будет высшего качества. Вероятность того, что изделие не высшего качества, равна q=1p=10,6=0,4.
Для вычисления вероятностей того, что из n изделий k изделий высшего качества воспользуемся формулой Бернулли:
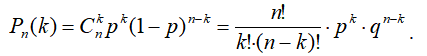
Наход...
