В каждом из 510 независимых испытаний событие A происходит с постоянной вероятностью p равно 0,41. Найдите вероятность того, что событие A происходит: а) точно 230 раз;

Число испытаний n = 510.

p = P(A) = 0,41 q = 1 - p = 0.59

Так как число испытаний велико, то вероятность того, что в n независимых повторных испытаниях событие наступит ровно раз, найдем с помощью локальной теоремы Лапласа:

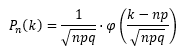
локальная функция Лапласа. Данная функция четная. Значения берем из таблицы значений локальной функции Лапласа