В заданиях вычислить интеграл точно по формуле Ньютона-Лейбница и приближенно по формулам прямоугольников. Отрезок интегрирования разбить на десять частей. Найти абсолютную и относительную погрешность результата вычислений.
- Высшая математика
Условие:
В заданиях вычислить интеграл 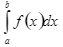 точно по формуле Ньютона-Лейбница и приближенно по формулам прямоугольников. Отрезок интегрирования разбить на 10 частей. Все вычисления проводить, сохраняя четыре знака после запятой. Приближенное значение интеграла округлить до третьего десятичного знака. Найти абсолютную и относительную погрешность результата вычислений.
точно по формуле Ньютона-Лейбница и приближенно по формулам прямоугольников. Отрезок интегрирования разбить на 10 частей. Все вычисления проводить, сохраняя четыре знака после запятой. Приближенное значение интеграла округлить до третьего десятичного знака. Найти абсолютную и относительную погрешность результата вычислений.
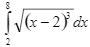
Решение:
Вычислим интеграл по формуле Ньютона-Лейбница:
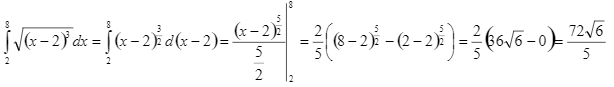
Вычислим интеграл приближенно по формулам прямоугольников. Существует 3 модификации:
1) метод левых прямоугольников;
2) метод правых прямоугольников;
3) метод средних прямоугольников.
Рассмотрим их по отдельности:
1) Метод левых прямоугольников.
Если функция f(x) непрерывна на отрезке [a; b] и он разбит на n равных частей: то определенный интеграл можно вы...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства