Заданное уравнение линии 2-го порядка привести к каноническому виду и построить кривую в системе координат ОXY. Указать: 1) канонический вид уравнения линии; 2) преобразование параллельного переноса, приводящее к каноническому виду; 3) в случае эллипса:
- Высшая математика
Условие:
Заданное уравнение линии 2-го порядка привести к каноническому виду и построить кривую в системе координат ОXY.
Указать:
1) канонический вид уравнения линии;
2) преобразование параллельного переноса, приводящее к каноническому виду;
3) в случае эллипса: полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки С до фокусов, написать уравнения правой и нижней частей кривой;
в случае гиперболы: полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки С до фокусов, уравнения асимптот, написать уравнения левой и верхней частей кривой;
в случае параболы: параметр, вершину, фокус, уравнение директрисы, расстояния от точки С до фокуса и директрисы, написать уравнения правой или нижней (в зависимости от положения кривой) частей кривой.
Для точки С проверить свойство, характеризующее данный тип кривых как ГМТ.
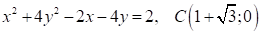
Решение:
Выделим последовательно полные квадраты:
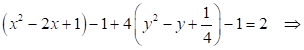
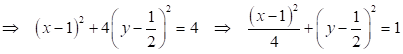
Выполним параллельный перенос:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства