Условие:
Исходные данные
Задан объект управления в виде передаточной функции
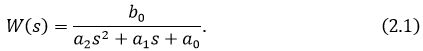
Коэффициенты приведены в табл.2.1.

Требуется выполнить:
1) Найти дифференциальное уравнение, соответствующее (2.1).
2) Представить найденное дифференциальное уравнение в пространстве состояний.
3) Составить структурную схему дифференциального уравнения по п.2.
4) Составить блок-схему для (2.1) со своими коэффициентами и набрать ее в среде моделирующей программы VisSim.
5) Получить переходную функцию и фазовый портрет системы (2.1) со своими коэффициентами. Фазовый портрет должен состоять из восьми фазовых траекторий, соответствующих разным начальным значениям при нулевом входном сигнале. Начальные точки должны находиться в четырех квадрантах фазовой плоскости. Начальные точки устанавливать, изменяя начальные значения интеграторов системы.
6) Изменяя a1, получить аналогичным образом временные диаграммы и фазовый портрет системы для следующих видов переходной функции:
а) апериодический устойчивый (устойчивый узел);
б) колебательно сходящейся, не менее четырех колебаний (устойчивый фокус);
в) на границе устойчивости (центр);
г) колебательно расходящейся (неустойчивый фокус);
д) апериодический неустойчивый (неустойчивый узел).
е) апериодический неустойчивый (седло). При получении седла можно изменять и a2.
Решение:
1. При заданных значениях коэффициентов передаточная функция запишется в виде:
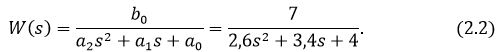
Передаточной функции соответствует следующее ДУ:
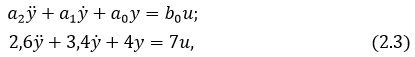
где выходной сигнал и его производные по времени; u управляющее воздейст...
