Условие:
Исходные данные для расчета:
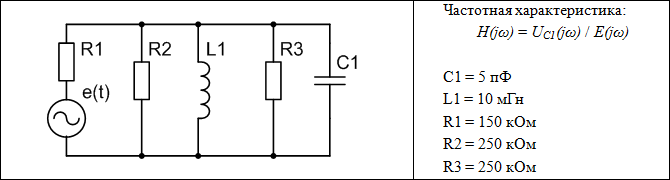
1. По исходным данным определить теоретическое значение резонансной частоты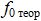 
заданной цепи.
2. Получить аналитическое выражение для комплексной частотной характеристики (КЧХ) цепи.
3. Получить аналитическое выражение модуля КЧХ – амплитудно-частотной характеристики (АЧХ) цепи.
4. Аналитически определить значение АЧХ при значениях частоты, равной:
- 0;
- резонансной частоте;
- бесконечности.
Учесть, что при нулевой частоте индуктивность это провод, конденсатор разрыв цепи, а при бесконечности, наоборот.
5. По аналитическому выражению из п. 3 построить график АЧХ.
6. По графику АЧХ определить резонансную частоту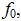 
граничные частоты полосы пропускания 
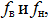а также ширину полосы пропускания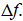 
7. Получить аналитическое выражение аргумента КЧХ – фазо-частотной характеристики (ФЧХ) цепи.
8. По аналитическому выражению из п. 7 построить график ФЧХ.
9. По графику ФЧХ определить резонансную частоту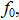 
граничные частоты полосы пропускания 
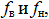а также ширину полосы пропускания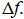 
Решение:
1. В заданной схеме катушка индуктивности L1 и конденсатор C1 включены параллельно. В этом случае резонансная частота определяется равенством реактивных проводимостей этих элементов.
На частоте резонанса можем записать:
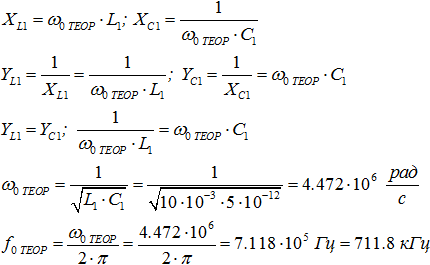
2. Получаем выражение для комплексной частотной характеристики.
Для упрощения расчетов обозначаем: