Условие задачи
Вычисление координат съемочного обоснования
Увязка углов хода. Значения измеренных углов и величины горизонтальных проложений записывают в графу 2 и 7 ведомости вычисления координат (табл. 5). Вычисляют сумму Σβпр. измеренных углов замкнутого хода (полигона). Определяют теоретическую сумму углов Σβт = 1800(n – 2), где n — число вершин хода.
Примечание. При нахождении суммы Σβпр. используются только внутренние углы пятиугольника. Углы висячего хода на точках ПТ16 и ст. I (βПТ и β1прим ) в данной задаче не увязываются.
Отсюда угловая невязка будет равна: fβ = Σβпр. - Σβт. = Σβпр. – 5400
Если невязка fβ не превышает допустимой величины доп.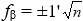 
, то ее распределяют с обратным знаком поровну на все углы хода,
то есть δβ =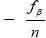 
с округлением значений поправок до десятых долей минут.
Исправленные указанными поправками углы записывают в графу 3 ведомости. Сумма исправленных углов должна равняться теоретической.
После этого приступают к вычислению дирекционных углов и румбов сторон хода. Для этого необходимо знать исходный дирекционный угол α0, для чего решается обратная геодезическая задача.
Ответ
Сущность этой задачи сводится к определению направления (дирекционного угла) прямой линии по известным координатам ее концов (рис. 5).
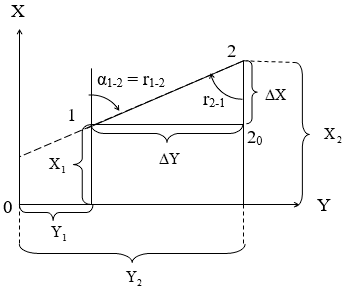
Рис. 5. Схема решения обратной геодезической задачи
Из рис.5 следует, что угол r2-1 треугольника 1220 противолежащий катету 120 (приращению ) есть не что иное, как румб линии 2-1, который по абсолютной величине равен накрест лежащему углу r1-2, т.е. румбу искомой лин...
