Условие:
Движение точки задано уравнениями в декартовых координатах x=f1(t), y=f2(t), z=f3(t) (x, y, z в см, t в с). Определить величину и направление скорости и ускорения точки и радиус кривизны траектории в момент времени t1.
Исходные данные: x=t3-4, см; y=sin (пt/3), см; z=cos2пt, см; t1 = 2с.
Решение:
Проекции скорости на координатные оси:
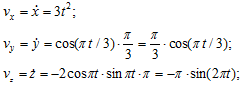
В момент времени t1 = 2c:
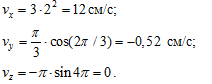
Модуль скорости точки в данный момент времени:
