1. Главная
  2. Библиотека
  3. Сопротивление материалов
  4. Для заданной стальной балки требуется: Определить опорные реакции. Построить эпюры поперечных сил Qy и изгибающих моментов...

Для заданной стальной балки требуется: Определить опорные реакции. Построить эпюры поперечных сил Qy и изгибающих моментов Mz. Подобрать поперечные сечения балки.

«Для заданной стальной балки требуется: Определить опорные реакции. Построить эпюры поперечных сил Qy и изгибающих моментов Mz. Подобрать поперечные сечения балки.»
  • Сопротивление материалов

Условие:

Для заданной стальной балки, при условии, что P=ql и M=ql2

Требуется: 

1. Определить опорные реакции. 

2. Построить эпюры поперечных сил Qy и изгибающих моментов Mz. 

3. Подобрать поперечные сечения балки: круглое диаметра d, прямоугольное с отношением высоты к ширине h/b=2 и двутавровое.

4. Для сечения балки, расположенного над любой опорой, построить эпюры нормальных и касательных напряжений для 3-х видов сечений. Для двутаврового сечения провести анализ напряженного состояния в точке перехода полки в стенку в зоне растяжения на уровне минимальной ширины подобранного поперечного сечения. Определить величину и направление главных напряжений и показать на выделенном элементе положение главных площадок. 

5. Определить, линейное в точке 1 и угловое в сечении 2, перемещения с помощью интеграла Мора. 

Исходные данные: схема; q=70 кН/м; l=0,8 м; P=ql=56 кН; M=ql2=44,8 кН·м; [σ]=160 МПа.

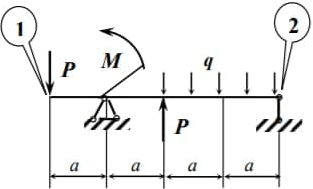
Схема к задаче

Решение:

1. Определим опорные реакции:

mA=Pl+M+Pl -q2l2l+RB3l=0

Откуда RB=18,77 кН

Fy=RA-P+P-q2l+RB=0

Откуда RA=93,33 кН

Проверка:

mB=P4l+M-RA3l-P2l+q2ll-M=0

2. Определяем внутренние усилия. Проведем сечения на каждом характерном участке и рассмотрим равновесие отсеченных частей.

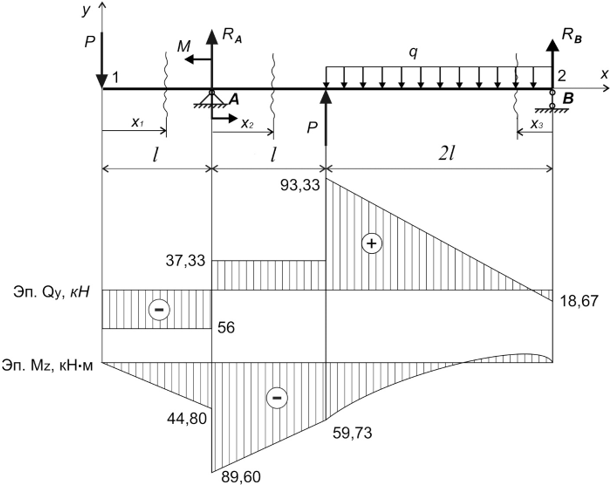
Участок I:

Qy=-P=-56 кН

Mz=-Px1

x1=0 Mz=0

x1=0,8 м Mz=-560,8=-44,80 кНм

Участок II:

Qy=RA-P=37,33 кН

Mz=-Pl+x2+RAx...-M

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я