Условие:
Пластина вращается вокруг неподвижной оси с постоянной угловой скоростью ω, заданной в таблице (при знаке минус направление ω противоположно показанному на рисунке). Ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости). По пластине вдоль прямой BD движется точка М; закон ее относительного движения задается уравнением s=AM=f(t) (s - в сантиметрах, t - в секундах). На рисунках точка М показана в положении, при котором s = AM > 0 (при s < 0 точка М находится по другую сторону от точки А).
Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t1=1c.

Исходные данные: 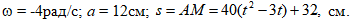
Решение:
Движение точки М является сложным. Оно складывается из относительного движения прямолинейного движения по линии ВD, и переносного движения вращения вместе с пластиной относительно оси О (рис. 7).
Определим положение точки на линии ВD в момент времени t = 1с:
![]()
Длина половины диагонали АВ -
