По заданным уравнениям движения точки x = f1(t), y = f2(t) найти уравнение траектории точки. Для момента времени t1=1 с вычислить ее скорость, нормальное, касательное и полное ускорения, а также радиус кривизны траектории.

По заданным уравнениям движения точки x = f₁(t), y = f₂(t) найти уравнение траектории точки. Для момента времени t₁=1с вычислить ее скорость, нормальное, касательное и полное ускорения, а также радиус кривизны траектории. На рисунке в масштабе изобразить траекторию движения точки и для заданного момента времени t₁=1с построить векторы скорости и ускорения.

Уравнения движения точки x = f₁(t) указаны на соответствующих рисунках, а уравнения движения y = f₂(t) приведены в табл. К1 величины х и у измеряются в см, время в секундах.

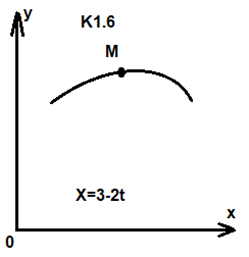
Таблица К1 Уравнения движения точки y = f₂(t)