Условие задачи
Из множества 6-значных номеров 000000-999999 случайным образом выбирается один номер. Рассматриваются события:
A = {каждая цифра номера встречается дважды};
B = {номер содержит только 4 различных цифры};
С = {сумма цифр номера равна 8}.
1) Выбрать соответствующее множество в качестве пространства элементарных исходов рассматриваемого испытания и с помощью его элементов описать события А, В, С
2) Проверить попарную несовместность событий А, В, С
3) Проверить, образуют ли события А, В, С полную группу событий
4) Используя классическое или геометрическое определение вероятности, найти вероятности событий А, В, С
5) Используя теоремы сложения и умножения найти Р(А+В), Р(А+ВС), Р(А+В+С), 
6) Проверить парную и взаимную независимость событий А, В, С
Ответ
1. Всего существует 1 000 000 исходов:
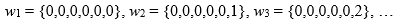
То есть элементарный исход имеет вид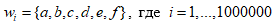 
номер элементарного исхода, цифра, стоящая на первом, втором, третьем, четвертом, пятом и шестом местах соответственно.
