1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. По  выборке  двухмерной  случайной  величины,  которая содержит 50 пар значений (x, y), – вычислить точечную оценку коэффи...

По  выборке  двухмерной  случайной  величины,  которая содержит 50 пар значений (x, y), – вычислить точечную оценку коэффициента корреляции; – вычислить интервальную оценку коэффициента корреляции (γ = 0,95);

«По  выборке  двухмерной  случайной  величины,  которая содержит 50 пар значений (x, y), – вычислить точечную оценку коэффициента корреляции; – вычислить интервальную оценку коэффициента корреляции (γ = 0,95);»
  • Теория вероятностей

Условие:

 По  выборке  двухмерной  случайной  величины,  которая содержит 50 пар значений (x, y),

– вычислить точечную оценку коэффициента корреляции;

– вычислить интервальную оценку коэффициента корреляции (γ = 0,95);

– проверить гипотезу об отсутствии корреляционной зависимости (α = 0,05);

– вычислить оценки параметров a0* и a1* линии регрессии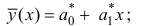

– построить диаграмму рассеивания и линию регрессии.  

Решение:

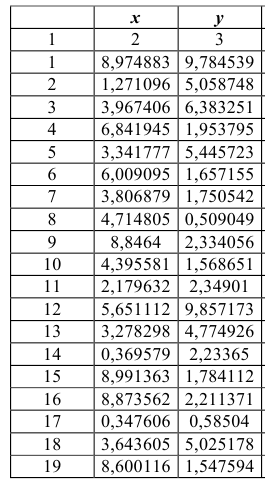
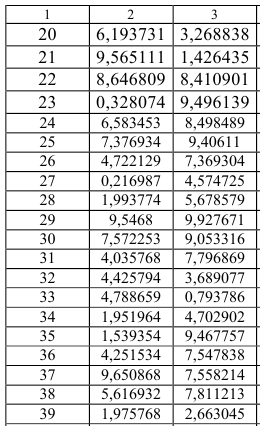
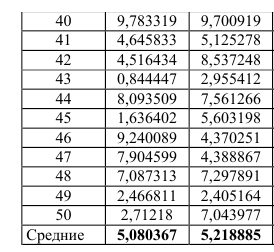
Для решения задачи удобно воспользоваться табл. 1. Значения в 3, 4 и 5-м столбцах вычисляются по формулам, приведенными в головке таблицы. В последней строке таблицы приведены средние арифметические значений каждого из столбцов.

Таким образом получены:

оценки математических ожиданий по каждой переменной (см. табл. 1):

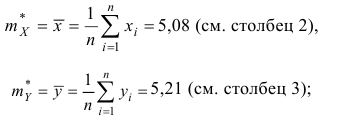
оценки начальных моментов второго порядка по каждой переменной:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я