Решение задачи
На ребре АА1 куба ABCDA1B1C1D1 взята точка A2 – середина этого ребра. Считая ребро куба равным а, найдите расстояние между прямой p=В1 A2 и прямой q=АС
- Геометрия
Условие:
На ребре АА1 куба ABCDA1B1C1D1 взята точка A2 – середина этого ребра. Считая ребро куба равным а, найдите расстояние между прямой p=В1A2 и прямой q=АС.
Исходные данные:
ABCDA1B1C1D1 – куб;
AB=a;
AA2=A2A1;
p=В1A2;
q=АС;
Найти: d(p,q)=?
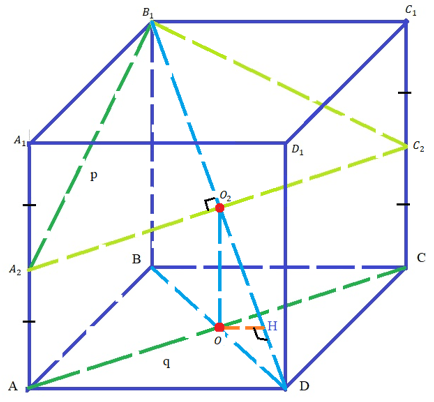
Решение:
1) Проведем отрезок A2 C2, соединяющий середины ребер AA1 и CC1. Получим прямоугольник AA2 C2 C.
2) Центр куба лежит в серединах отрезка A2 C2 и диагонали B1 D.
3) AC∥A2 C2 AC∥(A2 B1 C2). Следовательно, расстояние между прямыми AC и A2 B1 равно расстоянию между прямой AC (любой точкой этой прямой) и плоскостью...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э