Условие задачи
Стальной вал постоянного сечения вращается с частотой n (об/мин) и передаёт мощность N(кВт). Требуется подобрать диаметр вала из условия его прочности при совместном действии изгиба и кручения, если известны предел текучести материала и коэффициент запаса прочности.
Таблица 8. Исходные данные
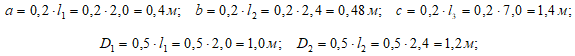
Требуется:
1. Определить моменты, приложенные к шкивам, по заданным «N» и «n».
2. Построить эпюру крутящих моментов «Мк».
3. Определить окружные усилия, действующие на шкивы, по найденным моментам и заданным диаметрам D1 и D2.
4. Определить давление на вал, принимая их равными трём окружным усилиям.
5. Определить силы, изгибающие вал в горизонтальной и вертикальной плоскостях (вес шкивов и вала не учитывать.
6. Построить эпюры изгибающих моментов от горизонтальных сил Му и от вертикальных сил Мz; (для каждого поперечного сечения имеется своя плоскость действия суммарного изгибающего момента; но для круглого сечения можно совместить плоскости изгибающих моментов для всех поперечных сечений и построить суммарную эпюру в плоскости чертежа; при построении эпюры надо учесть, что для некоторых участков вала она не будет прямолинейной);
8. По эпюрам крутящих моментов МКР и изгибающим моментам найти опасное сечение и определить наибольший расчётный момент по третьей теории прочности;
9. Подобрать диаметр вала «d» при допускаемом напряжении:
И округлить его значение до ближайшего равного: 30,40, 45, 50, 60, 70, 80, 90, 100 мм.
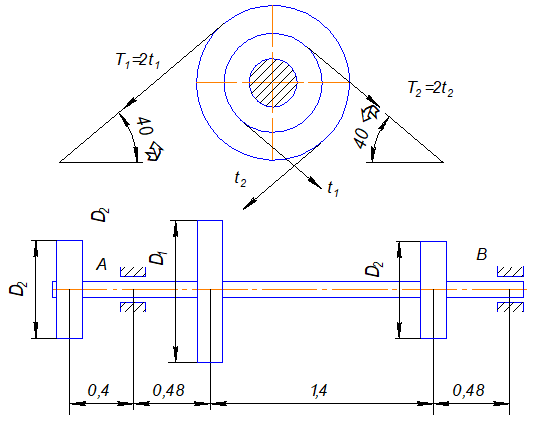
Рис.17 Схема вала.
Ответ
1. Нагрузки, действующие на вал:
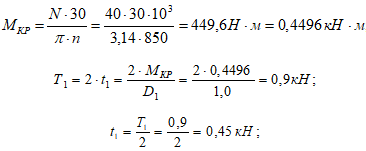
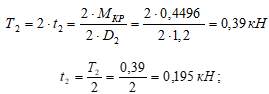
Усилие Т2 - действует на каждый шкив диаметром D2
