Условие задачи
Брак при изготовлении штампованных деталей составляет 5%. Сколько нужно взять деталей, чтобы наиболее вероятное число годных деталей равнялось 10? Какому распределению подчиняется случайная величина Х, равная числу годных деталей, и чему равно ее математическое ожидание и дисперсия?
Ответ
Данное распределение является биномиальным, математическое ожидание и дисперсия которого равны: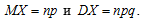 
Биномиальное распределение позволяет, в частности, установить, какое число появлений события А наиболее вероятно по формуле:
Потяни
