Решение задачи
Даны результаты наблюдений случайной величины икс. Разделив интервал значений икс на 10 равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, найти оценки математического ожидания и дисперсии случайной величины.
- Теория вероятностей
Условие:
Даны результаты наблюдений случайной величины X. Разделив интервал значений X на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, найти оценки математического ожидания и дисперсии исследуемой случайной величины. На основе этих построений выдвинуть гипотезу о законе распределения X и на графике гистограммы изобразить выравнивающую кривую. На уровне значимости α=0,05 по критерию χ2 Пирсона установить согласие или несогласие выдвинутой гипотезы с результатами наблюдений.
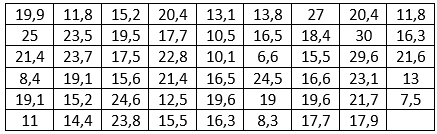
Решение:
n = 53 объем выборки.
Упорядочив выборку по возрастанию, получим вариационный ряд:
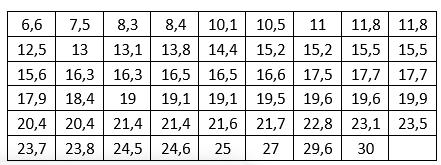
k = 10 число интервалов.
xmin = 6,6 наименьшее значение выборки.
xmax = 30 наибольшее значение выборки.
Длина интервалов:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э