Условие задачи
1. На стоянке свободно 6 мест. Два автомобиля синего цвета и четыре автомобиля красного цвета должны припарковаться на свободные места.
Сколько способов заполнения стоянки существует, если автомобили синего цвета будут парковаться друг с другом?
2. В корзине лежит 5 красных шаров, 4 белых шара и 3 черных шара. Ольга достает из корзины 4 шара. Сколько комбинаций, состоящих из четырех шаров возможно, если среди шаров, которые достала Ольга, будет больше 2 белых шаров?
Ответ
1. Так как два синие автомобили всегда паркуются рядом, будем рассматривать их как один, соответственно будем рассматривать число размещение 2 автомобилей на 5 местах. Определим число:
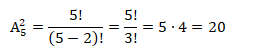
Поскольку мы рассматривали два синих автомобиля как один, а их порядок также может быть различным, при этом существует два варианта их размещение, число размещений 3 автомобилей будет равно
